Let $f(x)$ be an even function, integrable in $\left [ 0,\alpha \right ]$ and $g(x)$ another function such that $g(-x)=\frac{1}{g(x)}$, $g(x)\neq0$, $g(x)\neq-1$ in $\left [ -\alpha,\alpha \right ]$.
It can be proved that:
$$\int_{-\alpha }^{\alpha }\frac{f(x)}{1+g(x)}dx=\int_{0}^{\alpha}f(x)dx (1)$$
It turns out to be an interesting formula in the sense that it allows to simplify and speed up some integrals calculations.
Let’s see some examples.
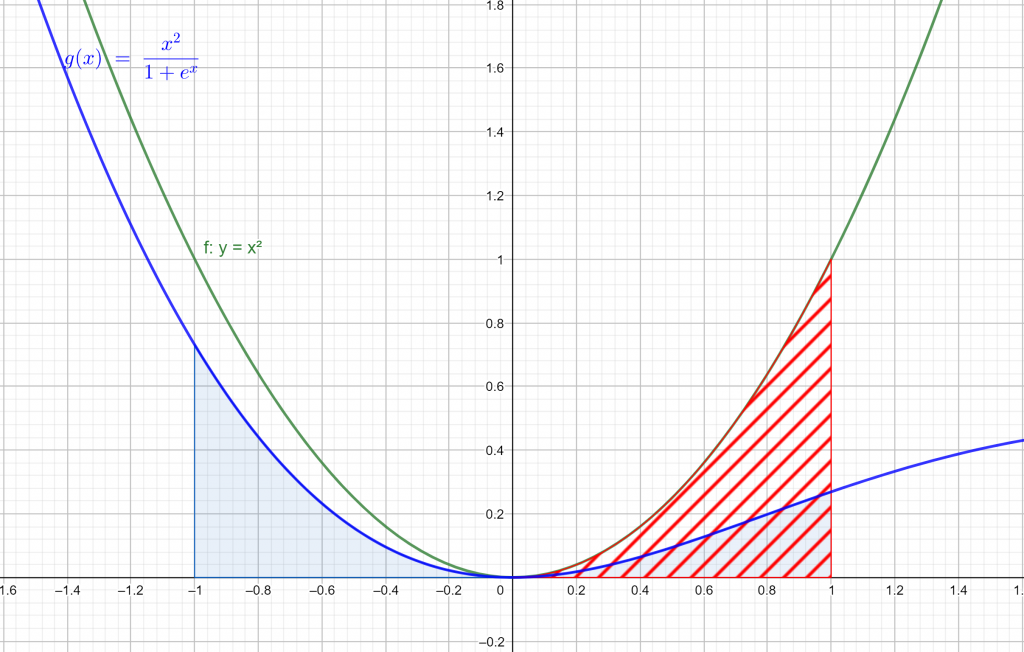
1. Let $f(x)=x^2$ and $g(x)=e^x$. In this case (1) becomes $$\int_{-1}^{1}\frac{x^2}{1+e^x}dx=\int_{0}^{1}x^2dx=\left [ \frac{1}{3}x^3 \right ]_{0}^{1}=\frac{1}{3}$$
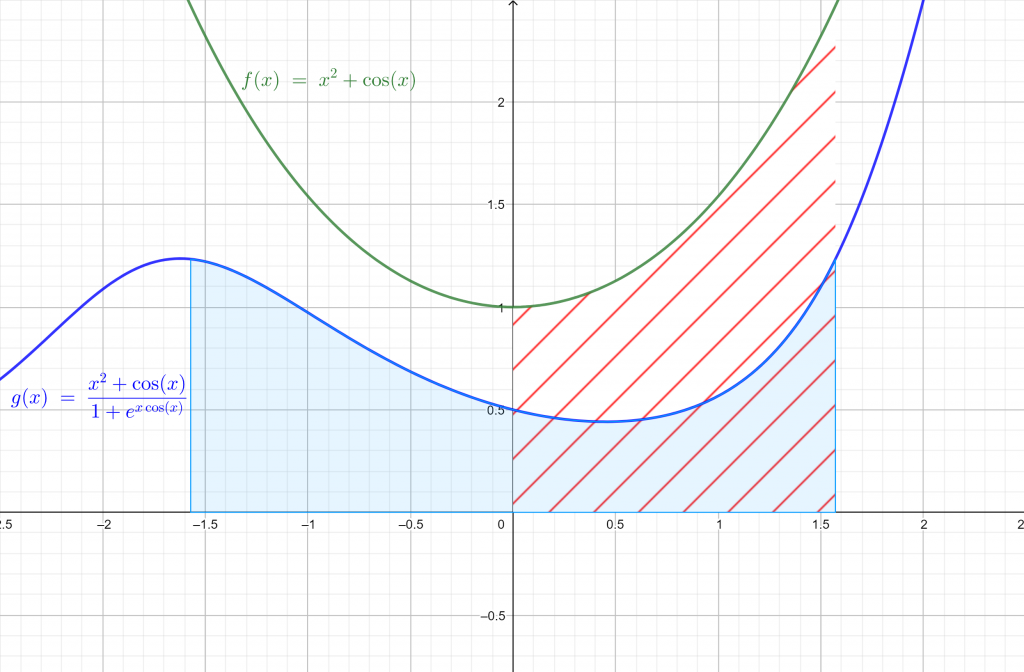
2. Let now $f(x)=x^2+cosx$ and $g(x)=e^{xcosx}$. We have$$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{x^2+cosx}{1+e^{xcosx}}dx=\int_{0}^{\pi/2}(x^2+cosx)dx=\left [ \frac{1}{3}x^3 +sinx\right ]_{0}^{\pi/2}=\frac{\pi}{24}+1$$
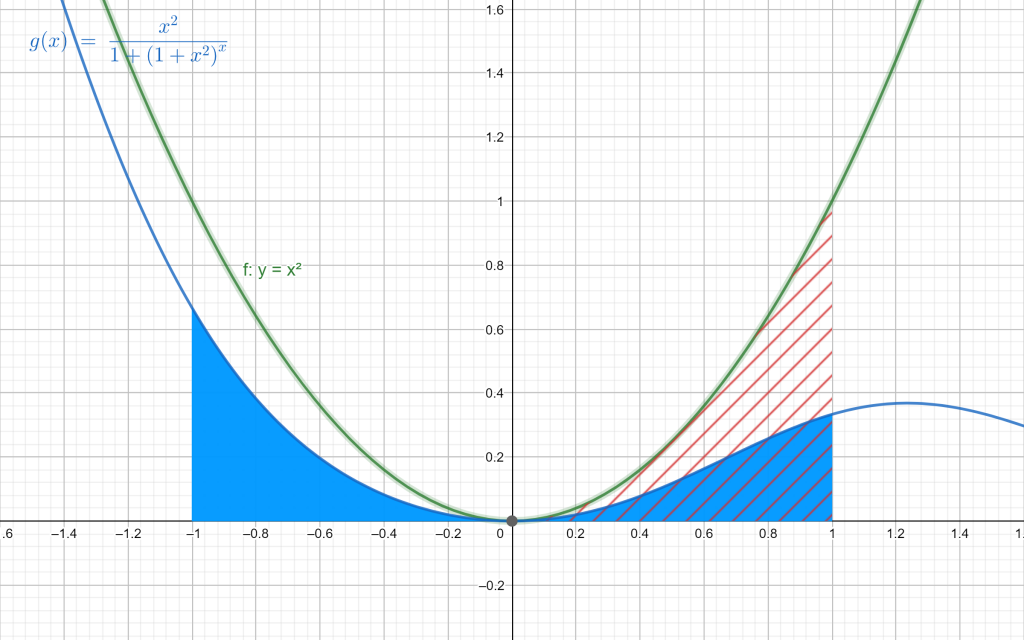
3. Finally, let $f(x)=x^2$ and $g(x)=(1+x^2)^x$. Formula (1) becomes$$\int_{-1}^{1}\frac{x^2}{1+(1+x^2)^{x}}dx=\int_{0}^{1}x^2dx=\left [ \frac{1}{3}x^3\right ]_{0}^{1}=\frac{1}{3}$$
Proof
It’s a straightforward calculation.
$$\int_{-\alpha }^{\alpha }\frac{f(x)}{1+g(x)}dx=\int_{-\alpha }^{0}\frac{f(x)}{1+g(x)}dx+\int_{0}^{\alpha }\frac{f(x)}{1+g(x)}dx=$$
$$=\int_{-\alpha }^{0}\frac{f(x)\frac{1}{g(x)}}{1+\frac{1}{g(x)}}dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=\int_{-\alpha }^{0}\frac{f(x)(\frac{1}{g(x)}+1-1)}{1+\frac{1}{g(x)}}dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=$$
$$=\int_{-\alpha }^{0}\left [f(x)-\frac{f(x)}{1+\frac{1}{g(x)}} \right ]dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=\int_{-\alpha }^{0}f(x)dx-\int_{-\alpha }^{0}\frac{f(x)}{1+\frac{1}{g(x)}}dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=$$
applying the variable change $t=-x$ ($dt=-dx$) in the second integral and using the fact that $f(x)$ is even in the first integral,
$$=\int_{0}^{\alpha}f(x)dx-\int_{0}^{\alpha}\frac{f(t)}{1+g(t)}dt+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=\int_{0}^{\alpha}f(x)dx$$
and the formula is proven.