In this brief article, we’ll see how to find the equivalent resistance of the following net:
Let’s call REQ the equivalent resistance we’re requested to evaluate.
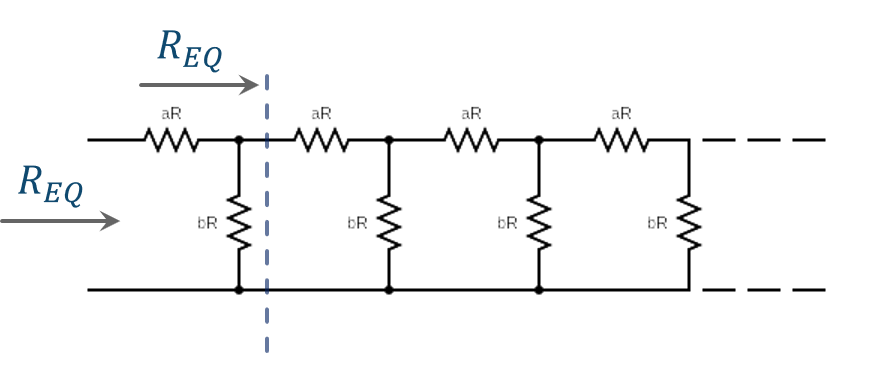
If we cut the net as indicated by the dotted arrow in the picture below, we can observe that the equivalent resistance of the part of the net on the right of the dotted line is again REQ
So, we can write:
$R_{EQ}=aR+bR||R_{EQ}$,
$R_{EQ}=aR+\frac{bR\cdot R_{EQ}}{bR+{R_{EQ}}}$,
$(bR+R_{EQ})R_{EQ}=aR(bR+R_{EQ})+bRR_{EQ}$ (*)
Going on with some algebra and solving the quadratic equation, we have:
$R_{EQ}=\frac{aR}{2}(1+\sqrt{1+\frac{4b}{a}})$ (1)
Let’s have now a glance to few special cases.
- $a=0$. In this case, all the $aR$ resistances are short circuits, that means that the overall resistance will be zero. Indeed, if we put $a=0$ in (*) we get $R_{EQ}=0$.
- $b=0$. In this case, all the $bR$ resistances will be 0, therefore all the resistors on the right of the first $bR$ will be shorted. Hence, the overall equivalent resistance will be only $aR$. Indeed, if we put $b=0$ in (1), we get $R_{EQ}=aR$.
- Finally, let’s consider the case $a=b\neq0$. If we substitute in (1), we quickly have:
$R_{EQ}=\frac{1+\sqrt{5}}{2}R \cong 1.618R$ (2)
Many of you should have noticed the “golden number” ($\frac{1+\sqrt{5}}{2}$) in (2). It seems it’s hidden everywhere…
Let’s see another way to get the same result as (2), which should provide another reason why the “golden number” is appearing in the equivalent resistance expression.
Let’s build the equivalent resistance step by step. Let’s recall we’re now considering the net made by all equale resistors ($R$)
In the first step, let’s calculate the equivalent resistance as if the net was made of the first 2 resistors only. It is:
$R_{EQ,1}=2R=\frac{2}{1}R$
In the second step, let’s add one couple of resistors (one series and one parallel). We have:
$R_{EQ,2}=R+R||2R=R+\frac{2R^{2}}{3R}=\frac{5}{3}R$
In the third step, let’s add one more couple of resistors (one series and one parallel). We have:
$R_{EQ,3}=R+R||(R+R||2R)=R+R||\frac{5}{3}R=R+\frac{(\frac{5}{3}R^{2})}{\frac{8}{3}R}=R+\frac{5}{8}R=\frac{13}{8}R$
Going on few steps, we’ll get the following sequence:
$\left \{R_{EQ,n}\right \}=\left \{ \frac{2}{1}R, \frac{5}{3}R, \frac{13}{8}R, \frac{34}{21}R, … \right \}$
This should remind us the Fibonacci’s sequence:
$f_{n}=\left \{ 1,1,2,3,5,8,13,21,34,55,… \right \}$
In fact, we have
$\left \{R_{EQ,n}\right \}=\left \{ \frac{f_{2n+1}}{f_{2n}}R \right \}$ (3)
Now, since the sequence (3) is a sub-sequence of $\left \{ \frac{f_{n+1}}{f_{n}}R \right \}$ (i.e. the sequence of ratios of 2 adjacent Fibonacci’s sequence terms) whose limit is the golden number, we have:
$R_{EQ}=\lim_{n}R_{EQ,n}=\lim_{n}\frac{f_{2n+1}}{f_{2n}}R=\lim_{n}\frac{f_{n+1}}{f_{n}}R=\frac{1+\sqrt{5}}{2}R$,
which is the same result as (2).

But in reality the whole net grip is something like that and it’s working, so how can be this right?
Sorry I caanot catch your comment. I can’t understand what a net grip is. Please explain better your comment.