Sia $f(x)$ una funzione pari, integrabile in $\left [ 0,\alpha \right ]$ e $g(x)$ una funzione tale che $g(-x)=\frac{1}{g(x)}$, $g(x)\neq0$, $g(x)\neq-1$ in $\left [ -\alpha,\alpha \right ]$.

Si può dimostrare che:

$$\int_{-\alpha }^{\alpha }\frac{f(x)}{1+g(x)}dx=\int_{0}^{\alpha}f(x)dx (1)$$

È una formula molto interessante in quanto permette di semplificare e velocizzare il calcolo di alcuni integrali definiti.

Prima della dimostrazione vediamo qualche esempio.

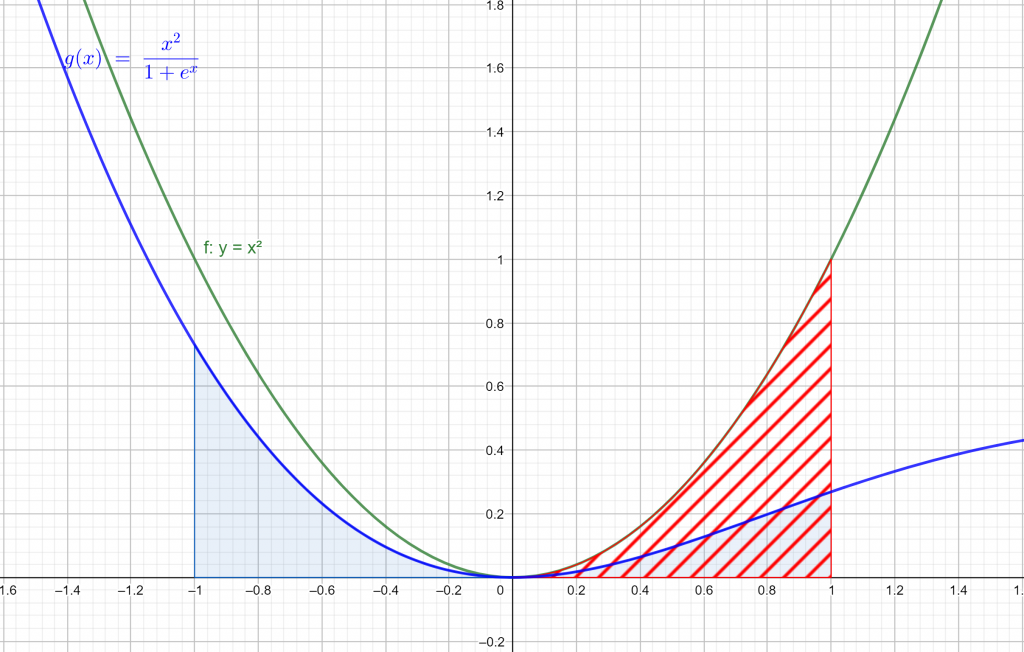
1. Sia $f(x)=x^2$ e $g(x)=e^x$. In questo caso la (1) diviene $$\int_{-1}^{1}\frac{x^2}{1+e^x}dx=\int_{0}^{1}x^2dx=\left [ \frac{1}{3}x^3 \right ]_{0}^{1}=\frac{1}{3}$$

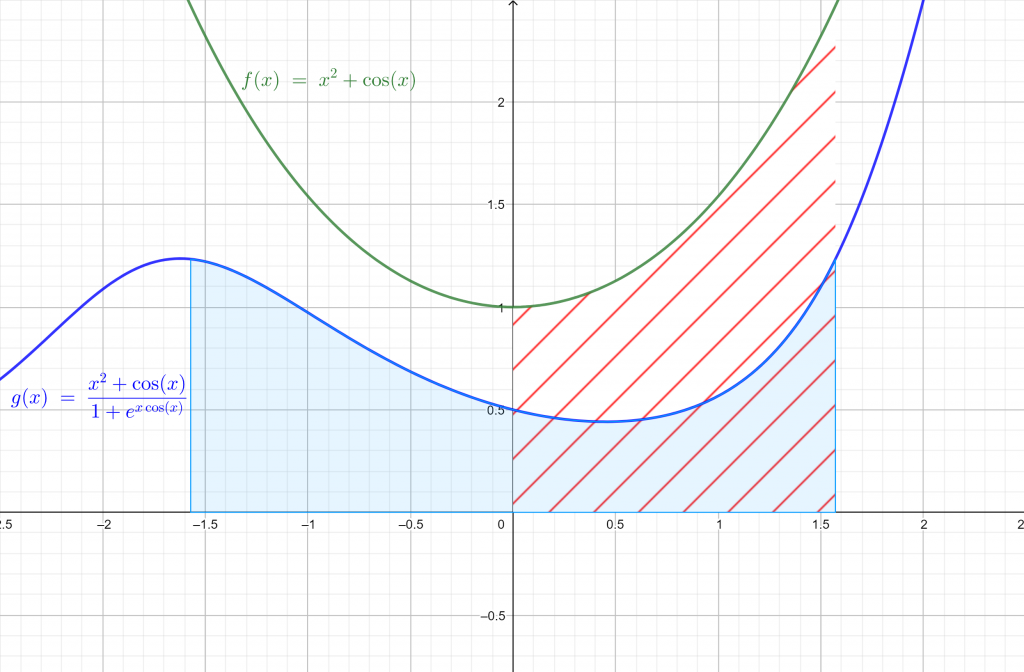
2. Sia ora $f(x)=x^2+cosx$ e $g(x)=e^{xcosx}$. Abbiamo$$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{x^2+cosx}{1+e^{xcosx}}dx=\int_{0}^{\pi/2}(x^2+cosx)dx=\left [ \frac{1}{3}x^3 +sinx\right ]_{0}^{\pi/2}=\frac{\pi}{24}+1$$

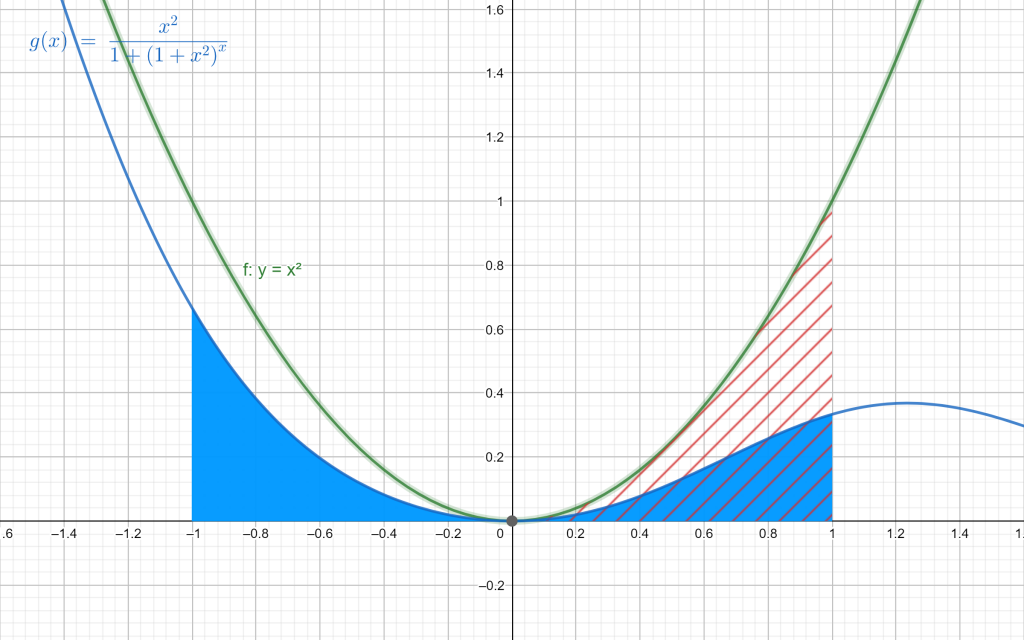
3. Infine, sia $f(x)=x^2$ e $g(x)=(1+x^2)^x$. La (1) diviene$$\int_{-1}^{1}\frac{x^2}{1+(1+x^2)^{x}}dx=\int_{0}^{1}x^2dx=\left [ \frac{1}{3}x^3\right ]_{0}^{1}=\frac{1}{3}$$

Dimostrazione

È un calcolo diretto dell’integrale definito.

$$\int_{-\alpha }^{\alpha }\frac{f(x)}{1+g(x)}dx=\int_{-\alpha }^{0}\frac{f(x)}{1+g(x)}dx+\int_{0}^{\alpha }\frac{f(x)}{1+g(x)}dx=$$

$$=\int_{-\alpha }^{0}\frac{f(x)\frac{1}{g(x)}}{1+\frac{1}{g(x)}}dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=\int_{-\alpha }^{0}\frac{f(x)(\frac{1}{g(x)}+1-1)}{1+\frac{1}{g(x)}}dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=$$

$$=\int_{-\alpha }^{0}\left [f(x)-\frac{f(x)}{1+\frac{1}{g(x)}} \right ]dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=\int_{-\alpha }^{0}f(x)dx-\int_{-\alpha }^{0}\frac{f(x)}{1+\frac{1}{g(x)}}dx+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=$$

applicando il cambio di variabile $t=-x$ ($dt=-dx$) nel secondo integrale e sfruttando la parità di $f(x)$ nel primo integrale,

$$=\int_{0}^{\alpha}f(x)dx-\int_{0}^{\alpha}\frac{f(t)}{1+g(t)}dt+\int_{0}^{\alpha}\frac{f(x)}{1+g(x)}dx=\int_{0}^{\alpha}f(x)dx$$

e la formula resta dimostrata.