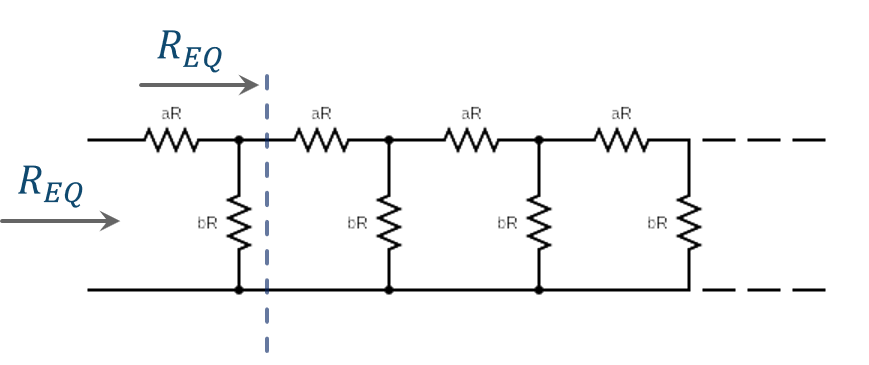
In queste poche righe vedremo come si può calcolare la resistenza equivalente della seguente rete costituita da infinite coppie di resistenze connesse in serie e in parallelo:
Indichiamo con $R_{EQ}$ la resistenza equivalente della rete di figura.
Se tagliamo idealmente la rete come indicato dalla linea tratteggiata nella figura sotto, è chiaro che la resistenza equivalente della rete a destra della linea è ancora la nostra $R_{EQ}$.
Abbiamo quindi:
$R_{EQ}=aR+bR||R_{EQ}$,
$R_{EQ}=aR+\frac{bR\cdot R_{EQ}}{bR+{R_{EQ}}}$,
$(bR+R_{EQ})R_{EQ}=aR(bR+R_{EQ})+bRR_{EQ}$ (*)
Con pochi passaggi algebrici e risolvendo l’equazione di secondo grado nella variabile $R_{EQ}$, si ha:
$R_{EQ}=\frac{aR}{2}(1+\sqrt{1+\frac{4b}{a}})$ (1)
Analizziamo brevemente alcuni casi particolari.
- $a=0$. In questo caso tutte le resistenze $aR$ sono cortocircuiti, quindi la resistenza equivalente attesa è nulla. Infatti, sostituendo $a=0$ nella (*) si ottiene $R_{EQ}=0$.
- $b=0$. In questo caso, tuttel el resistenze $bR$ sono dei cortocircuiti, quindi tutte le resistenze a destra della prima $aR$ saranno cortocircuitate. Pertanto, la resistenza equivalente complessiva è attesa essere $aR$. Infatti, sostituendo $b=0$ nella (1), si ottiene $R_{EQ}=aR$.
- Consideriamo infine il caso $a=b\neq0$. Sostituendo nella (1), si ha:
$R_{EQ}=\frac{1+\sqrt{5}}{2}R \cong 1.618R$ (2)
In molti avranno riconosciuto il numero aureo ($\frac{1+\sqrt{5}}{2}$) nella (2). Sembra che sia nascosto ovunque…
Vediamo un altro modo per ottenere lo stesso risultato della (2), che ci fornirà anche una ragione per cui il numero aureo appare nella (2).
Costruiamo la resistenza equivalente ad un passo per volta. Ricordiamo che stiamo calcolando la $R_{EQ}$ nel caso della rete con tutte le resistenze uguali tra loro ($R$)
Al primo step, calcoliamo la resistenza equivalente della rete costituite solo dalle prime due resistenze:
$R_{EQ,1}=2R=\frac{2}{1}R$
Al secondo step, aggiungiamo una coppia di resistenze (una in serie, l’altra in parallelo):
$R_{EQ,2}=R+R||2R=R+\frac{2R^{2}}{3R}=\frac{5}{3}R$
Al terzo step, aggiungiamo un’altra coppia di resistenze (una in serie, l’altra in parallelo):
$R_{EQ,3}=R+R||(R+R||2R)=R+R||\frac{5}{3}R=R+\frac{(\frac{5}{3}R^{2})}{\frac{8}{3}R}=R+\frac{5}{8}R=\frac{13}{8}R$
È evidente che stiamo ottenendo la seguente successione:
$\left \{R_{EQ,n}\right \}=\left \{ \frac{2}{1}R, \frac{5}{3}R, \frac{13}{8}R, \frac{34}{21}R, … \right \}$
Questa successione ci ricorda la successione di Fibonacci:
$f_{n}=\left \{ 1,1,2,3,5,8,13,21,34,55,… \right \}$
Infatti:
$\left \{R_{EQ,n}\right \}=\left \{ \frac{f_{2n+1}}{f_{2n}}R \right \}$ (3)
Ora, poiché la successione (3) è una estratta della $\left \{ \frac{f_{n+1}}{f_{n}}R \right \}$ (i.e. la successione dei rapporti dei termini consecutivi della successione di Fibonacci) che tende al numero aureo, si ha:
$R_{EQ}=\lim_{n}R_{EQ,n}=\lim_{n}\frac{f_{2n+1}}{f_{2n}}R=\lim_{n}\frac{f_{n+1}}{f_{n}}R=\frac{1+\sqrt{5}}{2}R$,
che coincide con la (2).